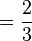miércoles, 28 de octubre de 2009
la raiscuadrada
Ejemplo ilustrativo:
Hallar la raíz cuadrada de 623 y expresar el resultado con dos cifras decimales.
Solución:
Escribimos el número, cuya raíz queremos calcular, bajo el signo radical:
Escribimos un par de ceros, a la derecha del número, por cada cifra decimal que queremos hallar, y un par adicional para aproximar la segunda cifra decimal:
Separamos en períodos, con apóstrofos ( ' ), las cifras de dos en dos, comenzando por la derecha:
Extraemos la raíz cuadrada entera del número en el primer período de la izquierda (6), ésta será la primera cifra de la raíz; la ubicamos en la casilla del resultado:
Se eleva al cuadrado la cifra obtenida en el paso anterior y, dicho cuadrado, se resta del número en el primer período:
Se baja el segundo período y, se separa con un apóstrofo la última cifra del número resultante:
Multiplicamos por dos el número que tenemos hasta ahora en la casilla del resultado:
Si el número formado a la izquierda del apóstrofo (22) es menor que el duplo del número que tenemos en la raíz (calculado en el paso anterior), ponemos un cero en la raíz. No es este el caso en el presente ejercicio, pués 22>4. Seguimos: si el número escrito antes del apóstrofo es mayor o igual que el duplo de la raíz, lo dividimos por éste:
El cociente obtenido en el paso anterior, o una cifra menor, será la segunda cifra de la raíz.
Para probar si el cociente anterior es la cifra correcta, se coloca a la derecha del duplo de la raíz hallada, y se multiplica por este mismo cociente. Si el producto es menor que el número del cual separamos la última cifra, éste es correcto y se sube a la raíz; en cambio, si el producto es mayor, se disminuye en una unidad o en más hasta que el producto sea menor:
Como 176 < 223, 4 es la cifra correcta; por lo que, la subimos a la raíz:
Efectuamos la resta entre el número que se forma cuando bajamos un período y el número correcto, hallado en la prueba anterior:
Bajamos el siguiente período y separamos con un apóstrofo la última cifra del número formado. Cuando bajamos el primer período de ceros (como es el caso presente), agregado por nosotros para obtener la primera cifra decimal, escribimos una coma en la raíz (comenzamos a encontrar los decimales):
Se repiten los pasos anteriores hasta concluir con el último período:
Duplicamos (multiplicamos por 2) el número que hasta este momento tenemos en la casilla del resultado, esto es, el 24:
48 < 470, y 48 en 470 está 9 veces; ensayemos con el 9:
4 401 < 4 700; 9 es la cifra correcta; escribimos 9 en la raíz:
Restamos 4 401 de 4 700, bajamos el siguiente período de ceros, separamos la última cifra del número formado y duplicamos el número presente en la raíz:
498 < 2 990, y 498 en 2 990 está 6 veces; ensayemos con el 6:
29 916 > 29 900, por lo que debemos disminuir a 6 en 1 y ensayar con 5:
24 925 < 29 900; Como 5 es la cifra correcta, la escribimos en la raíz:
Restamos 24 925 de 29 900, bajamos el siguiente período de ceros, separamos la última cifra del número formado y duplicamos el número presente en la raíz:
4 990 < 49 750, y 4 990 en 49 750 está 9 veces; ensayemos con el 9:
449 181 < 497 500; por lo tanto, el 9 es una cifra correcta y, la podríamos subir a la casilla del resultado; pero, como debemos dar la respuesta sólo con dos cifras decimales, este 9 nos indica que debemos aproximar a 6 la segunda cifra decimal.
De tal manera que, dada con dos cifras decimales:
martes, 27 de octubre de 2009
El eje de simetría es la mediatriz del segmento cuyos extremos son puntos simétricos.
Véase también [editar]
simetría
simetría radial
Transformación isométrica
isometría
Obtenido de "http://es.wikipedia.org/wiki/Eje_de_simetr%C3%ADa"
jueves, 15 de octubre de 2009
Jose Guadalupe Posada
Don Quijote
José Guadalupe Posada es considerado como artista
Comenzó su carrera haciendo dibujos , copiando imágenes religiosas y como ayudante de un taller de cerámica. Desde el estallido de la Revolución de 1910 hasta su muerte en el año de 1913, el maestro Posada trabajó incansablemente en la prensa dirigida a los trabajadores, ésta constituye hoy una crónica de la sociedad y la política de su época.
miércoles, 14 de octubre de 2009
EJES DE SIMETRIA
El eje de simetría es la mediatriz del segmento cuyos extremos son puntos simétricos.
Véase también [editar]
simetría
simetría radial
Transformación isométrica
isometría
Obtenido de "http://es.wikipedia.org/wiki/Eje_de_simetr%C3%ADa"
martes, 13 de octubre de 2009
los ejes de simetria
Un eje de simetría es una línea imaginaria que al dividir una forma cualquiera, lo hace en dos partes o mas, cuyos puntos simétricos son equidistantes entre sí.
El eje de simetría es la mediatriz del segmento cuyos extremos son puntos simétricos.
Véase también [editar]
simetría
simetría radial
Transformación isométrica
isometría
Obtenido de "http://es.wikipedia.org/wiki/Eje_de_simetr%C3%ADa"
lunes, 12 de octubre de 2009
sistema de numeracion binario
En una cifra binaria, cada digito tiene diferente valor dependiendo de la ocupacion que ocupe. El valor de cada posicion tiene una potencia de base 2, elevada a una exponente igual a la posicion menos uno. Se puede observar que la base de la potencia coincide con la cantidad de digitos utilizados (2) para representar los numeros.
Deacuerdo con estas reglas, el numero binario 1011 tiene un valor que se calcula asi:
3 2 1 0
1*2 + 0*2 +1*2 +1*2 , es decir
8+0+2+1= 11
y para expresar que ambas cifras describen la misma cantidad lo escribimos asi:
1011 = 11
2 10
Converciones entre numeros dacimales y binarios
Convertir un numero decimal a un numero binario es muy sencillo: basta con realizar diviciones sucesivas por 2 y escribir los restos obtenidos en cada divicion en orden inverso al que han sido obtenidos.
Por ejemplo, para convertir al sistema binario el numero 77 haremos una serie de diviciones arrojando los restos siguientes:
77 : 2 = 38 resto : 1
38 : 2 = 19 resto : 0
19 : 2 = 9 resto : 1
9 : 2 = 4 resto : 1
4 : 2 = 2 resto : 0
2 : 2 = 1 resto : 0
1 : 2 = 0 resto : 1
y tomando los restos en orden inverso obtenemos la cifra binaria:
77 = 1001101
10 2
COMO USAR EL ABACO MAYA
Sistema vigesimal
El sistema de numeración Maya era vigesimal, basado en el número 20, en vez de la base 10 usada actualmente.
En este último sistema hay diez cifras diferentes, 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 que se usan para representar cualquier número como potencias de la base del sistema, el número 10. Por ejemplo, el número 258 significa 2 x 102 + 5 x 101 + 8 x 100, es decir, dos centenas más cinco decenas más 8 unidades.
La notación en el sistema vigesimal es similar salvo que la base es 20. En este sistema se necesitan veinte cifras diferentes, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, y 19 que también se pueden representar como 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I y J. El número 6HF ó 6.17.15 significa, desde el punto de vista decimal 6 x 202 + 17 x 201 + 15 x 200 = 2755.
Según la posición las sucesivas cifras de cada número en el sistema decimal representan unidades, decenas, centenas, unidades de millar, etc; en el sistema vigesimal los nombres eran kines, uinales, tunes, etc. En la siguiente tabla se muestran algunos de los nombres:
Sistema decimal, base 10
Sistema vigesimal, base 20
Unidades
100 = 1
Kines
200 = 1
Decenas
101 = 10
Uinales
201 = 20
Centenas
102 = 100
Tunes
202 = 400
Unidades de millar
103 = 1000
Katunes
203 = 8000
Decenas de millar
104 = 10000
Baktunes
204 = 160000
Centenas de millar
105 = 100000
Pictunes
205 = 3200000
Unidades de millón
106 = 1000000
Calabtunes
206 = 64000000
Decenas de millón
107 = 10000000
Kinchiltunes
207 = 1280000000
Centenas de millón
108 = 100000000
Alautunes
208 = 25600000000
Luego el número 6HF representa 6 tunes más H uinales más F kines; o dicho de otra manera 6 tunes más 17 uinales más 15 kines.
En realidad el sistema Maya de numeración utilizado para cálculos calendáricos no era exactamente vigesimal, ya que cada tun equivalía a 18 uinales, pero aquí usaremos un sistema estrictamente vigesimal, totalmente regular y más apto para cálculos con el ábaco Nepohualtzintzin.
Los Mayas representaban los números de dos formas diferentes. Una de ellas era empleando 20 glifos diferentes que representan caras de perfil. Esta notación era usada en monumentos. La otra forma estaba constituida por puntos, con valor 1, y por rayas, con valor 5. El cero se representaba por medio del símbolo de una concha.
Si el número estaba formado por más de una cifra, se colocaban verticalmente, con los kines en la parte inferior.
Abaco Nepohualtzintzin
Con el sistema numérico vigesimal los Mayas podían efectutar las operaciones matemáticas fundamentales por medio de tablas de sumar y de multiplicar y con la utilización de un ábaco constituido por una cuadrícula hecha con varillas, o dibujado directamente en el suelo, y se utilizaban piedrecillas o semillas para representar los números. Este ábaco recibía el nombre de Nepohualtzintzin.
En la parte superior de cada varilla tiene tres cuentas, cada una de ellas con valor de cinco unidades (una mano). En la parte inferior hay cuatro cuentas, cada una de ellas con valor de una unidad (un dedo). Las cuentas sólo tienen valor cuando están apoyadas en la barra central.
Una construcción moderna y utilizable del ábaco Nepohualtzintzin es el mostrado en la imagen, construido por el autor de esta página. Su manejo es similar al del ábaco Japonés Soroban, aunque tiene dos cuentas más con valor 5 debido a que se opera en el sistema vigesimal. En la imagen se muestra el número 38C (ó 3.8.12), cuyo valor en el sistema decimal es 1372.
En el Nepohualtzintzin de la imagen, con 8 varillas, se podrían hacer cálculos con números inferiores a JJJJJJJJ (ó 19.19.19.19.19.19.19.19) que en el sistema decimal es 25 599 999 999.
Además, si se dejan sin uso las dos cuentas o bolas superiores, se puede usar como si fuese un Soroban en el sistema decimal. Conviene profundizar en el estudio de las operaciones en el sistema decimal usando un Soroban antes de abordar las operaciones en el sistema vigesimal en un Nepohualtzintzin. De este modo se podrá hacer la transición con facilidad. Cualquier operación que se pueda hacer en un Soroban se puede hacer en un Nepohualtzintzin, la metodología es similar, sólo al principio operar en el sistema vigesimal resulta un poco extraño por no estar acostumbrados a él y no sabernos las tablas de sumar y de multiplicar de memoria, como sí ocurre en el sistema decimal estudiado desde la infancia en las escuelas.
Es fácil construir un Nepohualtzintzin con básicos conocimientos de bricolage, pero también se puede construir simplemente cambiando la posición de la barra central de un ábaco Chino Suanpan, que tiene disposición de cuentas 2/5, para dejarlo en la disposición 3/4 del ábaco Nepohualtzintzin.
Puede practicar con un ábaco Nepohualtzintzin virtual accesible aquí. Se necesita tener instalado JAVA. El programa permite usar todo tipo de ábacos reales o incluso otros según las preferencias del usuario. Para usar un Nepohualtzintzin elija la opción Japanese y la base 20. En la barra central hay un cursor que marca la posición del punto o coma que separa la parte entera del número de la decimal (mejor dicho: vigesimal), puede moverlo con el ratón al lugar deseado.
El máximo honor que se puede hacer a los conocimientos de otras civilizaciones es no olvidarlos. El ábaco Nepohualtzintzin merece un lugar junto al Soroban Japonés, el Suanpan Chino, el Schoty Ruso y otras variantes de los anteriores.
SERIES BNUMERICAS
- ______/________/_______/_________/_____________/__________/
1/3 2/3 5/3
CLACIFICA EN LA RECTA NUMERICA 1/3 ,2/3,5/3.
SI PUEDES VER EN LA RECTA LA SERIE VA DE 1/3 EN 1/3.
sábado, 10 de octubre de 2009
Pues estaba observando el contenido y lo que han subido y me parece que esta excelente.
En este primer periodo me parece que pues ya hasta lo ultimo le empezaron a poner ganas a esto del blog no quisiera pensar que solo lo van a subir ya a la mera hora osea cuando ya van a entregar las calificaciones, es mejor comenzar desde el principio.
Bueno pues ya me voy a mi blog y les recuerdo que no se olviden de subir información y de antemano felicitarlos a los poquitos pero significativos integrantes de este el mejor blog de primero.
Bueno me despido y que en Matemáticas y en las demás materias que tengan salgan de lo mejor en este su primer periodo de primer año en la secundaria.
adiós!!!!!
viernes, 9 de octubre de 2009
ejercicio
18/9, 45/28, 6/9, 19/56, 1/4.
Resuelve los siguientes problemas.
En laa escuela secundaria A, cada 5 leen el periodico y 26 no lo hacen. En la secuundaria B, 6 si lo hacen y 22 no ¿ En que secundaria hay mayor interes por leer el periodico?
R. el A
Un joven fue a comprar 1 1/2 litros de aceite; en la tienda en contro varias opciones:
a) Mraca Cielo 1/2 litro $5.50 b)Marca Nube 3/4 litro a $7.20
c) Marca Estrella 1 litro a $12.00 d)Marca Sol 1 1/2 litros a $15.25
Al llegar a casa, su madre lo felicito por comprar el mas barato ¿Cual fue la marca que comrpo?
R. La marca nube
Numeración egipcia
De Wikipedia, la enciclopedia libre
El sistema de numeración egipcio permitía representar números, desde el uno hasta millones, desde el inicio del uso de la escritura jeroglífica. A principios del tercer milenio a. C. los egipcios disponían del primer sistema desarrollado decimal –numeración de base 10. Aunque no era un sistema posicional, permitía el uso de grandes números y también describir pequeñas cantidades en forma de fracciones unitarias: las fracciones del Ojo de Horus.
| Valor | 1 | 10 | 100 | 1.000 | 10.000 | 100.000 | 1 millón, o infinito | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jeroglífico |
|
|
|
|
|
o
|
| ||||||||||||||||
| Descripción | Trazo vertical (bastoncito) | Asa o herradura invertida | Cuerda enrollada (espiral) | Flor de loto con tallo. | Dedo | Renacuajo o rana. | Hombre arrodillado con las manos levantadas |
| Los demás valores se expresaban con la repetición del símbolo, el número de veces que fuera necesario. Por ejemplo, el bajorrelieve de Karnak, que habla del botín de Thutmose III (siglo XV a. C.) (Museo del Louvre, París), muestra el número 4622 como: |
| Está escrito de izquierda a derecha y de arriba a abajo pero en el grabado original en piedra están de derecha a izquierda y los signos están invertidos (los signos jeroglíficos podían ser escritos en ambas direcciones, de derecha a izquierda o de izquierda a derecha, incluso verticalmente). FraccionesegipciaArtículo principal: Fracción egipcia Los números racionales también podían ser expresados, pero sólo como sumas de fracciones unitarias, con la unidad por numerador, excepto para 2/3 y 3/4. El indicativo de fracción es representado por el jeroglífico de la boca (R), y significa "parte":
Las fracciones se escribían con este operador, p.e. el numerador 1, y el denominador positivo debajo. Así, 1/3 se escribía:
Había signos especiales para 1/2, para 2/3 (de uso frecuente) y 3/4 (de uso menos frecuente):
Si el "denominador" era muy grande y el signo de la "boca" no cabía encima, esta se situaba justo encima del comienzo del "denominador". Aparte de 2/3 y 3/4 los egipcios no conocían fracciones con numerador distinto a uno. Por ejemplo, la fracción 3/5 se representaba como 1/2 + 1/10 y similar a este ejemplo se descomponían todas las fracciones como suma de fracciones con la unidad como numerador.
|
miércoles, 7 de octubre de 2009
LAS SERIES NUMERICAS
4,8,12,16:20,24,28,32,36.B)
Como puede verce en la recta numerica la A va de 2 en 2 y la B va de 4 en 4.
series de numeros
martes, 6 de octubre de 2009
ABACO MAYA
-vigesimal
Basado en el numero:
-20.
En vez de la base usada actualmente,que es
la base del numero :
-10.
En este último cistema hay
-10 cifras diferentesque son:
-0
-1
-2
-3
-4
-5
-6
-7
-8
-9.
Que se usan para representar cualquier númerocomo potensias de la base del sistema el número 10.
FRACCIONES DECIMALES Y SECUENCIAS

_/_____________u_______C_______/______________________________/
d 1
ubica en las recta lo siguiente: 1/4, 3/8, 4/8.
un cuarto:U
tres octavos:C