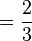lunes, 21 de diciembre de 2009
¿Como sacar el area de un circulo?
Ejemplo:
El area de un circulo con un diametro de 6cm, su radio seria de 3cm la mitad y segun la formula 3.14 por el cudrado de 3cm que seria 9( multiplicado por si mismo) entonces el area del circulo seria 28.26
examen en limpio (quebrados)
LOS QUEBRADOS SE PUEDEN SIMPLIFICAR O AMPLIFICAR .
EN 3/5 EL 5 SERIA EL DENOMINADOR Y EL 3 EL NUMERADOR.
- 6/10 x 12/8=
martes, 15 de diciembre de 2009
EJERCICIO
círculo
perímetro
diámetro
¿Cómo se llama la line que va del centro de la circunferencia hasta cualquier extremo de la misma ?
diámetro
radio
área
perímetro
¿Cómo se llama el número especial que los Griegos?descubrieron como la relacion que existe entre lacircunferencia y el diámetro?
pi
17
316
número primo
¿Cuál es el valor de pi?
13.1416
3.14163.
1614
ninguno de los tres
¿Cuál de estos símbolos hace referencia a pi ?
el símboloπ
el símbolo£
el símbolo∑
el símbolo€
RESPUESTAS DEL EXAMEN ANTERIOR
R= 1.55
2.-la mitad de la estatura de Pablo es la medida de sus pantalones. ¿Cuanto miden sus pantalones en cm.?
R= 68.5
3.- si se cuenta de2 en 2 se realizan 5 conteos para llegar al 10. si se cuenta de 3 en 3 se realizan 4 conteos para sobrepasar el 10 por primera vez. Si se cuenta de1.5 en 1.5, ¿Cuantos conteos se tienen que hacer para sobrepasar 10 por primera vez?
R= 4
4.- si cuentas de 2.25 en 2.25, ¿cuantos conteos se tienen que hacer para sobrepasar 10 por primera vez?
R= 5
5.- tenemos una tabla de triplay de 2 m. por lado , es decir, una pieza de 4 m. cuadrados de area y luego se corta una pieza de 1.5 m. por 1.5 m. ¿Que area tiene la pieza cortada?
R= 2.25 m. cadrados.
6.- ¿Cuanta madera sobra del problema anterior?
R= 1.75 m. cuadrados.
7.- en las sig. multilpicaciones elige el lugar donde debe estar el punto decimal (preguntas 7 y 8 ).
7.925 * 5.94= 44707450
R= 47.07450
8.- 72.52 * 22.94= 16549064
R=1654.9064
9.- en las sig. diiviciones elige el lugar donde debe estar el punto decimal.
576 / 4.2= 13800
R=138.00
10.- 123.6 / 42.2 = 29289
R=292.89
11.- multiplpica 0.25 * 0.25 * 0.25 =
R=0.015625
12.- un rectangulo tiene de area 16 cm.cuadrados y su base mide 2.2 cm. ¿Cuanto mide la altura?
R=7.27
13.- ¿Cuantos dolares de estados unidos se podian compra con $3500 si cada dolara costaba $10.94 (hasta decimos)?
R= 319.9 dolares.
14.- ¿Cuantos quetzales de guatemala se pueden comprar con $440 si cada quetzal cuesta $1.40 pesos mexicanos ?
R= 314.28
15.- la moneda de peru se llama nuevo sol y por cada $3.40 pesoos podemos obtener un nuevo sol. ¿Cuantos ppodemos obtener con $500?
R=1.4705 nuevos soles
16.- un litro dse gasolina cuesta $8.22 el tanque del auto de Miguel Brito se llena con 48 litros : ¿Cuanto se debe pagar por llenar el tanque?
R= $394.56
17.- cada mes el precio de la gasolina aumenta 0.02. ¿Cuanto debera pagar de mas el prosimo mes por llenar el tanque?
R=$0.96
18.- ¿Dentro de cuantos meses se pagara por primera vez mas de $400 por llenar gasolina?
R= 6
19.- siete amigos fueron al cine y en total pagaron $300.00 ¿Cuanto le toco aportar a cada uno?
R= $42.90
20.- un deportista camina 4 1/2 kilometros diarios en 1/4 de horas. Si avanza a velocidad constante, ¿Cuanto recorrera en una hora?
R= 3.6 hrs.
correccion del examen
R.: 68.5CM
2
2:UN RECTANGULO TIENE DE AREA 16CM Y7 BASE 2.2
¡CUANTO MIDE LA ALTURA?
R:7.27CM
3 :UNA VENTANA CUADRADA TIENE DE AREA 6889 SE VA A REFORZAR CONUNA TIRA DE ALUMINIO EN LA BASE ¿ CUANTO DEBE MEDIR LA LATITUD ?
R:83CM
BUSCAR UN NUMERO QUE MULTIPLICADO POR SI MISMO DE EL AREA
QUE ME PIDEN.
lunes, 14 de diciembre de 2009
la raiz cuadeada
- PROBLEMAS ,Y SE REPRESENTA x .
- SE PONE EN FORMA DE CASITA.
- SIRVE PARA MUCHAS COSA COMO ASERCAMIENTOS.
sábado, 12 de diciembre de 2009
circunferencia
Si medimos con un hilo la longitud de la circunferencia, veremos que es igual a 3,14 su diametro. A este número decimal se lo define con la letra griega “pi”.
Dimensión de la circunferencia:
Al ser una línea, la circunferencia tiene una sola dimensión, la longitud.
Una circunferencia está formada por:
Centro de la circunferencia: punto del que equidistan todos los puntos de la circunferencia.
Radio de la circunferencia: segmento que une el centro de la circunferencia con cualquier punto de la misma.
Cuerda de la circunferencia: segmento que une dos puntos de la circunferencia, el radio es perpendicular a la cuerda en su punto medio.
Diámetro de la circunferencia: es una cuerda que pasa por el centro. Es la cuerda que mayor tamaño tiene.
Arco de la circunferencia: es la porción de circunferencia limitada por dos puntos de la misma, también se puede decir que es cada una de las partes en que una cuerda divide a la circunferencia.
CIRCULO
En castellano, la palabra círculo tiene varias acepciones, la primera:[1] una superficie geométrica plana contenida dentro de una circunferencia con área definida; mientras que se denomina circunferencia[2] a la curva geométrica plana, cerrada, cuyos puntos son equidistantes del centro, y sólo posee longitud. "Aunque ambos conceptos están relacionados, no debe confundirse la circunferencia (línea curva) con el círculo (superficie).
lunes, 7 de diciembre de 2009
NUMEROS DECIMALES
1
--- = 0.1
10
1
----- = 0.01
100
1
------ = 0.001
1000
263
----- = 2.63
100
54
---- = 0.54
100
domingo, 6 de diciembre de 2009
Operaciones con numeros decimales
Para sumar o restar en forma decimal se colocan los numeros de modo que las comas esten encolumnadas. Luego se suman o restan como si fueran numeros naturales, poniendo la coma en el resultado en su columna correspondiente.
Para multiplicar dos numeros decimales, se realiza la multiplicacion de ambos como si fueran numeros naturales. Luego se coloca la coma en el resultado, deparando tantas sifras como decimales tengan en conjunto los dos factores.
6.532 432 6.532 4.32 2.202
------- = ----- = ------- - ----- = --------
100 10 100 10 100
34.4 96.7 23.48
- 22.9 +96.9 * 1 .2
------- ---------- -------------
13.5 193 . 6 4696
2348
--------------
28.176
miércoles, 2 de diciembre de 2009
QUEBRADOS
5 1 10 3 10 + 3 13
-- + -- = -- + -- = ------- = ---
3 2 6 6 6 6
Restar quebrados o fracciones: lo mismo que la suma, pero al final en vez de sumar se restan . Por ejemplo:
6 4 18 4 18-3 14
-- + -- = --- + -- = ------- = ---
1 3 3 3 3 3
Multiplicar fraacciones o quebrados: es muy facil; se multiplican los numeradores para calcular
el nuevo numeror y se multiplican lo denominadores para calcular el nuevo denominador. Ejemplo:
3 1 3*1 3
-- * -- = ------- = ---
2 2 2*2 4
dividir quebrados o fracciones: tambien muy faciles de hacer. La vieja "se multiplican en cruz". es decir: el numerador se calcula multiplicando el primer el primer numerador por el segundo denominador. El denominador se calcula multiplicando el primer denominador por el segundo numerador. Ejemplo:
7 2 7*3 21
-- : -- = ------- = ---
5 3 5*2 10
martes, 10 de noviembre de 2009
miércoles, 4 de noviembre de 2009
Cuales son las ramas de las matematicas.
Estadistica.
Geometria.
Algebra
¿Que es arimetica?
Es el estudio de las estruturas numericas elementales, asi como las propiedades de las operaciones y los numeros en si mismos en su concepto mas profundo, construyendo lo que se conoce como teoria de numeros.
¿Que es la estadistica?
Es una ciencia con base matematica referente a la recoleccion de datos que busca explicar condiciones regulares en fenomenos de tipo aleatorio.
¿Que es geometria?
Es el estudio de las propiedades y de las medidas de las figuras en el plano o en el espacio.
¿Que es algebra?
Es el estudio de las operaciones. Una exprecion algebraica es una combinacion de variables, numeros y por lo menos una operacion.
y=3x+24.
miércoles, 28 de octubre de 2009
la raiscuadrada
Ejemplo ilustrativo:
Hallar la raíz cuadrada de 623 y expresar el resultado con dos cifras decimales.
Solución:
Escribimos el número, cuya raíz queremos calcular, bajo el signo radical:
Escribimos un par de ceros, a la derecha del número, por cada cifra decimal que queremos hallar, y un par adicional para aproximar la segunda cifra decimal:
Separamos en períodos, con apóstrofos ( ' ), las cifras de dos en dos, comenzando por la derecha:
Extraemos la raíz cuadrada entera del número en el primer período de la izquierda (6), ésta será la primera cifra de la raíz; la ubicamos en la casilla del resultado:
Se eleva al cuadrado la cifra obtenida en el paso anterior y, dicho cuadrado, se resta del número en el primer período:
Se baja el segundo período y, se separa con un apóstrofo la última cifra del número resultante:
Multiplicamos por dos el número que tenemos hasta ahora en la casilla del resultado:
Si el número formado a la izquierda del apóstrofo (22) es menor que el duplo del número que tenemos en la raíz (calculado en el paso anterior), ponemos un cero en la raíz. No es este el caso en el presente ejercicio, pués 22>4. Seguimos: si el número escrito antes del apóstrofo es mayor o igual que el duplo de la raíz, lo dividimos por éste:
El cociente obtenido en el paso anterior, o una cifra menor, será la segunda cifra de la raíz.
Para probar si el cociente anterior es la cifra correcta, se coloca a la derecha del duplo de la raíz hallada, y se multiplica por este mismo cociente. Si el producto es menor que el número del cual separamos la última cifra, éste es correcto y se sube a la raíz; en cambio, si el producto es mayor, se disminuye en una unidad o en más hasta que el producto sea menor:
Como 176 < 223, 4 es la cifra correcta; por lo que, la subimos a la raíz:
Efectuamos la resta entre el número que se forma cuando bajamos un período y el número correcto, hallado en la prueba anterior:
Bajamos el siguiente período y separamos con un apóstrofo la última cifra del número formado. Cuando bajamos el primer período de ceros (como es el caso presente), agregado por nosotros para obtener la primera cifra decimal, escribimos una coma en la raíz (comenzamos a encontrar los decimales):
Se repiten los pasos anteriores hasta concluir con el último período:
Duplicamos (multiplicamos por 2) el número que hasta este momento tenemos en la casilla del resultado, esto es, el 24:
48 < 470, y 48 en 470 está 9 veces; ensayemos con el 9:
4 401 < 4 700; 9 es la cifra correcta; escribimos 9 en la raíz:
Restamos 4 401 de 4 700, bajamos el siguiente período de ceros, separamos la última cifra del número formado y duplicamos el número presente en la raíz:
498 < 2 990, y 498 en 2 990 está 6 veces; ensayemos con el 6:
29 916 > 29 900, por lo que debemos disminuir a 6 en 1 y ensayar con 5:
24 925 < 29 900; Como 5 es la cifra correcta, la escribimos en la raíz:
Restamos 24 925 de 29 900, bajamos el siguiente período de ceros, separamos la última cifra del número formado y duplicamos el número presente en la raíz:
4 990 < 49 750, y 4 990 en 49 750 está 9 veces; ensayemos con el 9:
449 181 < 497 500; por lo tanto, el 9 es una cifra correcta y, la podríamos subir a la casilla del resultado; pero, como debemos dar la respuesta sólo con dos cifras decimales, este 9 nos indica que debemos aproximar a 6 la segunda cifra decimal.
De tal manera que, dada con dos cifras decimales:
martes, 27 de octubre de 2009
El eje de simetría es la mediatriz del segmento cuyos extremos son puntos simétricos.
Véase también [editar]
simetría
simetría radial
Transformación isométrica
isometría
Obtenido de "http://es.wikipedia.org/wiki/Eje_de_simetr%C3%ADa"
jueves, 15 de octubre de 2009
Jose Guadalupe Posada
Don Quijote
José Guadalupe Posada es considerado como artista
Comenzó su carrera haciendo dibujos , copiando imágenes religiosas y como ayudante de un taller de cerámica. Desde el estallido de la Revolución de 1910 hasta su muerte en el año de 1913, el maestro Posada trabajó incansablemente en la prensa dirigida a los trabajadores, ésta constituye hoy una crónica de la sociedad y la política de su época.
miércoles, 14 de octubre de 2009
EJES DE SIMETRIA
El eje de simetría es la mediatriz del segmento cuyos extremos son puntos simétricos.
Véase también [editar]
simetría
simetría radial
Transformación isométrica
isometría
Obtenido de "http://es.wikipedia.org/wiki/Eje_de_simetr%C3%ADa"
martes, 13 de octubre de 2009
los ejes de simetria
Un eje de simetría es una línea imaginaria que al dividir una forma cualquiera, lo hace en dos partes o mas, cuyos puntos simétricos son equidistantes entre sí.
El eje de simetría es la mediatriz del segmento cuyos extremos son puntos simétricos.
Véase también [editar]
simetría
simetría radial
Transformación isométrica
isometría
Obtenido de "http://es.wikipedia.org/wiki/Eje_de_simetr%C3%ADa"
lunes, 12 de octubre de 2009
sistema de numeracion binario
En una cifra binaria, cada digito tiene diferente valor dependiendo de la ocupacion que ocupe. El valor de cada posicion tiene una potencia de base 2, elevada a una exponente igual a la posicion menos uno. Se puede observar que la base de la potencia coincide con la cantidad de digitos utilizados (2) para representar los numeros.
Deacuerdo con estas reglas, el numero binario 1011 tiene un valor que se calcula asi:
3 2 1 0
1*2 + 0*2 +1*2 +1*2 , es decir
8+0+2+1= 11
y para expresar que ambas cifras describen la misma cantidad lo escribimos asi:
1011 = 11
2 10
Converciones entre numeros dacimales y binarios
Convertir un numero decimal a un numero binario es muy sencillo: basta con realizar diviciones sucesivas por 2 y escribir los restos obtenidos en cada divicion en orden inverso al que han sido obtenidos.
Por ejemplo, para convertir al sistema binario el numero 77 haremos una serie de diviciones arrojando los restos siguientes:
77 : 2 = 38 resto : 1
38 : 2 = 19 resto : 0
19 : 2 = 9 resto : 1
9 : 2 = 4 resto : 1
4 : 2 = 2 resto : 0
2 : 2 = 1 resto : 0
1 : 2 = 0 resto : 1
y tomando los restos en orden inverso obtenemos la cifra binaria:
77 = 1001101
10 2
COMO USAR EL ABACO MAYA
Sistema vigesimal
El sistema de numeración Maya era vigesimal, basado en el número 20, en vez de la base 10 usada actualmente.
En este último sistema hay diez cifras diferentes, 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 que se usan para representar cualquier número como potencias de la base del sistema, el número 10. Por ejemplo, el número 258 significa 2 x 102 + 5 x 101 + 8 x 100, es decir, dos centenas más cinco decenas más 8 unidades.
La notación en el sistema vigesimal es similar salvo que la base es 20. En este sistema se necesitan veinte cifras diferentes, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, y 19 que también se pueden representar como 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I y J. El número 6HF ó 6.17.15 significa, desde el punto de vista decimal 6 x 202 + 17 x 201 + 15 x 200 = 2755.
Según la posición las sucesivas cifras de cada número en el sistema decimal representan unidades, decenas, centenas, unidades de millar, etc; en el sistema vigesimal los nombres eran kines, uinales, tunes, etc. En la siguiente tabla se muestran algunos de los nombres:
Sistema decimal, base 10
Sistema vigesimal, base 20
Unidades
100 = 1
Kines
200 = 1
Decenas
101 = 10
Uinales
201 = 20
Centenas
102 = 100
Tunes
202 = 400
Unidades de millar
103 = 1000
Katunes
203 = 8000
Decenas de millar
104 = 10000
Baktunes
204 = 160000
Centenas de millar
105 = 100000
Pictunes
205 = 3200000
Unidades de millón
106 = 1000000
Calabtunes
206 = 64000000
Decenas de millón
107 = 10000000
Kinchiltunes
207 = 1280000000
Centenas de millón
108 = 100000000
Alautunes
208 = 25600000000
Luego el número 6HF representa 6 tunes más H uinales más F kines; o dicho de otra manera 6 tunes más 17 uinales más 15 kines.
En realidad el sistema Maya de numeración utilizado para cálculos calendáricos no era exactamente vigesimal, ya que cada tun equivalía a 18 uinales, pero aquí usaremos un sistema estrictamente vigesimal, totalmente regular y más apto para cálculos con el ábaco Nepohualtzintzin.
Los Mayas representaban los números de dos formas diferentes. Una de ellas era empleando 20 glifos diferentes que representan caras de perfil. Esta notación era usada en monumentos. La otra forma estaba constituida por puntos, con valor 1, y por rayas, con valor 5. El cero se representaba por medio del símbolo de una concha.
Si el número estaba formado por más de una cifra, se colocaban verticalmente, con los kines en la parte inferior.
Abaco Nepohualtzintzin
Con el sistema numérico vigesimal los Mayas podían efectutar las operaciones matemáticas fundamentales por medio de tablas de sumar y de multiplicar y con la utilización de un ábaco constituido por una cuadrícula hecha con varillas, o dibujado directamente en el suelo, y se utilizaban piedrecillas o semillas para representar los números. Este ábaco recibía el nombre de Nepohualtzintzin.
En la parte superior de cada varilla tiene tres cuentas, cada una de ellas con valor de cinco unidades (una mano). En la parte inferior hay cuatro cuentas, cada una de ellas con valor de una unidad (un dedo). Las cuentas sólo tienen valor cuando están apoyadas en la barra central.
Una construcción moderna y utilizable del ábaco Nepohualtzintzin es el mostrado en la imagen, construido por el autor de esta página. Su manejo es similar al del ábaco Japonés Soroban, aunque tiene dos cuentas más con valor 5 debido a que se opera en el sistema vigesimal. En la imagen se muestra el número 38C (ó 3.8.12), cuyo valor en el sistema decimal es 1372.
En el Nepohualtzintzin de la imagen, con 8 varillas, se podrían hacer cálculos con números inferiores a JJJJJJJJ (ó 19.19.19.19.19.19.19.19) que en el sistema decimal es 25 599 999 999.
Además, si se dejan sin uso las dos cuentas o bolas superiores, se puede usar como si fuese un Soroban en el sistema decimal. Conviene profundizar en el estudio de las operaciones en el sistema decimal usando un Soroban antes de abordar las operaciones en el sistema vigesimal en un Nepohualtzintzin. De este modo se podrá hacer la transición con facilidad. Cualquier operación que se pueda hacer en un Soroban se puede hacer en un Nepohualtzintzin, la metodología es similar, sólo al principio operar en el sistema vigesimal resulta un poco extraño por no estar acostumbrados a él y no sabernos las tablas de sumar y de multiplicar de memoria, como sí ocurre en el sistema decimal estudiado desde la infancia en las escuelas.
Es fácil construir un Nepohualtzintzin con básicos conocimientos de bricolage, pero también se puede construir simplemente cambiando la posición de la barra central de un ábaco Chino Suanpan, que tiene disposición de cuentas 2/5, para dejarlo en la disposición 3/4 del ábaco Nepohualtzintzin.
Puede practicar con un ábaco Nepohualtzintzin virtual accesible aquí. Se necesita tener instalado JAVA. El programa permite usar todo tipo de ábacos reales o incluso otros según las preferencias del usuario. Para usar un Nepohualtzintzin elija la opción Japanese y la base 20. En la barra central hay un cursor que marca la posición del punto o coma que separa la parte entera del número de la decimal (mejor dicho: vigesimal), puede moverlo con el ratón al lugar deseado.
El máximo honor que se puede hacer a los conocimientos de otras civilizaciones es no olvidarlos. El ábaco Nepohualtzintzin merece un lugar junto al Soroban Japonés, el Suanpan Chino, el Schoty Ruso y otras variantes de los anteriores.
SERIES BNUMERICAS
- ______/________/_______/_________/_____________/__________/
1/3 2/3 5/3
CLACIFICA EN LA RECTA NUMERICA 1/3 ,2/3,5/3.
SI PUEDES VER EN LA RECTA LA SERIE VA DE 1/3 EN 1/3.
sábado, 10 de octubre de 2009
Pues estaba observando el contenido y lo que han subido y me parece que esta excelente.
En este primer periodo me parece que pues ya hasta lo ultimo le empezaron a poner ganas a esto del blog no quisiera pensar que solo lo van a subir ya a la mera hora osea cuando ya van a entregar las calificaciones, es mejor comenzar desde el principio.
Bueno pues ya me voy a mi blog y les recuerdo que no se olviden de subir información y de antemano felicitarlos a los poquitos pero significativos integrantes de este el mejor blog de primero.
Bueno me despido y que en Matemáticas y en las demás materias que tengan salgan de lo mejor en este su primer periodo de primer año en la secundaria.
adiós!!!!!
viernes, 9 de octubre de 2009
ejercicio
18/9, 45/28, 6/9, 19/56, 1/4.
Resuelve los siguientes problemas.
En laa escuela secundaria A, cada 5 leen el periodico y 26 no lo hacen. En la secuundaria B, 6 si lo hacen y 22 no ¿ En que secundaria hay mayor interes por leer el periodico?
R. el A
Un joven fue a comprar 1 1/2 litros de aceite; en la tienda en contro varias opciones:
a) Mraca Cielo 1/2 litro $5.50 b)Marca Nube 3/4 litro a $7.20
c) Marca Estrella 1 litro a $12.00 d)Marca Sol 1 1/2 litros a $15.25
Al llegar a casa, su madre lo felicito por comprar el mas barato ¿Cual fue la marca que comrpo?
R. La marca nube
Numeración egipcia
De Wikipedia, la enciclopedia libre
El sistema de numeración egipcio permitía representar números, desde el uno hasta millones, desde el inicio del uso de la escritura jeroglífica. A principios del tercer milenio a. C. los egipcios disponían del primer sistema desarrollado decimal –numeración de base 10. Aunque no era un sistema posicional, permitía el uso de grandes números y también describir pequeñas cantidades en forma de fracciones unitarias: las fracciones del Ojo de Horus.
| Valor | 1 | 10 | 100 | 1.000 | 10.000 | 100.000 | 1 millón, o infinito | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jeroglífico |
|
|
|
|
|
o
|
| ||||||||||||||||
| Descripción | Trazo vertical (bastoncito) | Asa o herradura invertida | Cuerda enrollada (espiral) | Flor de loto con tallo. | Dedo | Renacuajo o rana. | Hombre arrodillado con las manos levantadas |
| Los demás valores se expresaban con la repetición del símbolo, el número de veces que fuera necesario. Por ejemplo, el bajorrelieve de Karnak, que habla del botín de Thutmose III (siglo XV a. C.) (Museo del Louvre, París), muestra el número 4622 como: |
| Está escrito de izquierda a derecha y de arriba a abajo pero en el grabado original en piedra están de derecha a izquierda y los signos están invertidos (los signos jeroglíficos podían ser escritos en ambas direcciones, de derecha a izquierda o de izquierda a derecha, incluso verticalmente). FraccionesegipciaArtículo principal: Fracción egipcia Los números racionales también podían ser expresados, pero sólo como sumas de fracciones unitarias, con la unidad por numerador, excepto para 2/3 y 3/4. El indicativo de fracción es representado por el jeroglífico de la boca (R), y significa "parte":
Las fracciones se escribían con este operador, p.e. el numerador 1, y el denominador positivo debajo. Así, 1/3 se escribía:
Había signos especiales para 1/2, para 2/3 (de uso frecuente) y 3/4 (de uso menos frecuente):
Si el "denominador" era muy grande y el signo de la "boca" no cabía encima, esta se situaba justo encima del comienzo del "denominador". Aparte de 2/3 y 3/4 los egipcios no conocían fracciones con numerador distinto a uno. Por ejemplo, la fracción 3/5 se representaba como 1/2 + 1/10 y similar a este ejemplo se descomponían todas las fracciones como suma de fracciones con la unidad como numerador.
|
miércoles, 7 de octubre de 2009
LAS SERIES NUMERICAS
4,8,12,16:20,24,28,32,36.B)
Como puede verce en la recta numerica la A va de 2 en 2 y la B va de 4 en 4.
series de numeros
martes, 6 de octubre de 2009
ABACO MAYA
-vigesimal
Basado en el numero:
-20.
En vez de la base usada actualmente,que es
la base del numero :
-10.
En este último cistema hay
-10 cifras diferentesque son:
-0
-1
-2
-3
-4
-5
-6
-7
-8
-9.
Que se usan para representar cualquier númerocomo potensias de la base del sistema el número 10.
FRACCIONES DECIMALES Y SECUENCIAS

_/_____________u_______C_______/______________________________/
d 1
ubica en las recta lo siguiente: 1/4, 3/8, 4/8.
un cuarto:U
tres octavos:C
sábado, 12 de septiembre de 2009
EL MEJOR GRUPO DE TODOS EL 1° D
miércoles, 10 de junio de 2009
EL CIRCULO
En castellano, la palabra círculo tiene varias acepciones, la primera[1] : una superficie geométrica plana contenida dentro de una circunferencia con área definida; mientras que se denomina circunferencia[2] a la curva geométrica plana, cerrada, cuyos puntos son equidistantes del centro, y sólo posee longitud.
Rectas y segmentos
Radio: es el segmento que une el centro con un punto de la circunferencia perimetral.
Diámetro: es el mayor segmento inscrito; pasa por el centro y divide al círculo dos semicírculos; es la mayor de las cuerdas de la circunferencia perimetral.
Cuerda: es el segmento que une los extremos de un arco.
Recta secante: es la recta que corta al círculo en dos partes de diferente área.
Recta tangente: es la recta que toca al círculo en un solo punto; es perpendicular al radio cuyo extremo es el punto de tangencia.
Recta exterior: es aquella recta que no toca ningún punto del círculo
TÉCNICA
1.-¿Cúal es la probabilidad que al soltar un dado caiga número non?
R= 1/2
2.-Es un sistema de cordenadas rectangulares que usamis para gráficar información :
R= plano cartesiano
3.- Una rueda gira y en cada vuelta avanza 2.4 m. ¿cúal es el diametro e esa rueda?
R= 76 cm
4.- ¿Como se llama el valor del plano cartesiano que corresponde a las cordenadas 0,0?
R= lugar de origen
5.- Analiza la siguiente información y analiza las siguientes preguntas:
x3x-3yx,y
6.-¿Cuanto vale y cuando x es igual a 3?
R= 4
7.-¿cuanto vale y cuando x vale 2?
R= 1
8.-¿cuanto vale y cuando x vale 1?
R= -2
9.-¿de cuanto en cuanto avanza o disminuye, de acuerdo a la tabla?
R= de 3 en 3
10.-¿cúal es la cordenada para la gráfica cuando x vale 0?
R= 0,-5
CRECIMIENTO EXPONENCIAL
En clase de matemáticas hemos visto gráficas con crecimiento lineal
como en la cual observamos que a mayor tiempo se recore mayor distancia
de una forma gradual en cambio en crecimiento exponencial no avanza de manera gradual sino de una forma muy acelerada y en muy poco tiempo se pueden obtener datos importantes.
Las bacterias tienen un crecimiento exponencial debido en que cada tiempo se duplica el número de bacterias después primero se producen dos, cuatro, seis, doce.
Los virus son más peligrosos por la base de su división no es el número 2, sino que puede ser cualquier otro, digamos, el seis. Así tendremos 6 a la siguiente 36 luego con 7776 con la capacidad de infectar.
RAÍZ CUADRADA
RAÍZ CUADRADA DE:551761=741
RAÍZ CUADRADA DE:2642=51
RAÍZ CUADRADA DE:484=22
RAÍZ CUADRADA DE:545=23
ECUACIONES
8(-8)=-64
-5+7(3+2)=30
32(+12)=-384
(-1.5)(4)=-6
8-3(2)=-2
72(+22)=1584
(+7)(-7)=+49
martes, 9 de junio de 2009
TÉCNICA
R= PARALELAS
Cual es el área de un triángulo de base 5/3 de metro y altura 3/2 expresa el resultado en fracción decimal
R: 1.2
Resuelve y simplifica : 4/8+2/5+1/3 = 37/30
¿Cúal es el valor de x en la ecuación x=200?
R= 30
4(125-223+100) = 28
-3 (-5-1-9) = 45
2(5-6) +-3(8-6) = -1
3
x +2 ¿cuanto vale ´´y´´cuando´´x´´ es igual a 5?
R= 127
lunes, 8 de junio de 2009
TECNICA
R: paralelas
Cual es el área de un triángulo de base 5/3 de metro y altura 3/2 expresa el resultado en fracción decimal
R: 1.2
Resuelve la siguiente operación y simplifica
4/8+2/5+1/3= 37/30
Cual es el valor de x en la ecuación 5x+50= 200
R: 30
12(-2+4)= 24
4(125-232+100)= -28
-3(-5-1-9)= 45
2(5-6)-3(8-6)= -2
--------------------
2(6-4)
La función es x3 +2
Cuanto vale Y cuando X es igual a 5
R: 127
lunes, 1 de junio de 2009
Plano Cartesiano
Un punto cualquiera de una recta puede asociarse y representarse con un número real, positivo si está situado a la derecha de un punto O, y negativo si esta a la izquierda. Dicho punto se llama centro de coordenadas O (letra O) y se asocia al valor 0 (cero).
Corresponde a la dimensión uno, que se representa con el eje X, en el cual definimos un centro de coordenadas, que se representa con la letra O (de Origen)
miércoles, 27 de mayo de 2009
EXAMEN DE DIAGNOSTICO
c) 142 800 000
Un automovil recorrió 480 km /h si denotamos con "x" el numero de horas que el auto estuvo en movimiento cual es la ecuación que corresponde a esta situación .
b) x=(480km)/(100km/h)
Una empresa registro en un mes ganancias por $500 000 y perdidas por $600 000, ¿cual numero expresa mejor el balanceo de esa empresa?
a)$100 000
Ines puso listón alrededor de una servilleta cuadrada, para lo cual uso 1.60m de listón ,si se llama "p" al lado de la servilleta ,¿cual ecuación corresponde a esta situación ?
d)4p=1.60
El hospedaje de 60 deportistas fue de $1800, si para los eventos de atletismo solamente se hospedan 40 atletas ¿cual se gastara?
d) $1200
Un carrito esta hecho a una escala de 1:25 si el original mide de largo 5 m ¿cuanto mide el carrito de largo ?
d)02m.
martes, 26 de mayo de 2009
TÉCNICA DEL 26 DE MAYO DEL 2009
1.- ¿Qué es y para que sirve un plano cartesiano?
R= sirve para representar gráficas
2.-¿Cómo se llama el lugar del plano cartesiano donde se cruzan los ejes y corresponde a la cordenada 0,0?
R= origen
3.-¿Cómo se llama el procedimiento usado para obtener valores y poderlos graficar?
R= tabulación
4.-¿Encuentra el valor de "y" cuando "x" vale 3?
R= -3
5.-¿Y cuando vale 2?
R=-1
6.-¿Y cuando vale 1?
R= +1
7.-Deacuerdo a la informacion anterior mientras la "x" disminuye de uno en uno ¿de cuanto en cuanto cambia la "y"?
R= de 2 en 2
8.-¿Qué tipo de relación existe entre "x" y "y"?
R= indirecta

¿QUÉ ES UN PLANO CARTESIANO?
miércoles, 20 de mayo de 2009
COMENTARIO DEL EXAMEN DE ENLACE
en mi punto de vista estuvo regular pero a mis
martes, 19 de mayo de 2009
¿Cómo fomentar la creatividad de los jóvenes?
Hola buenas noches:
A nosotros lo que nos a funcionado ha sido el tener contacto con gente tan entusiasta como ustedes o como los responsables del Clubhouse y desde luego sus pequeños socios. Con ellos hemos aprendido que soñar junto a los chavos y hacer realidad ese sueño es algo posible. Con ellos he conocido nuevas herramientas como Sctrach, que en la escuela donde trabajo se escuchaba más como estornudo. Digo Scrtach y no ha de faltar quien conteste ¡Salud!
La gente deja que otros piensen por ellos, eso no es más fácil que hacerlo por si mismo, pero lo parece. Las consecuencias son horribles. Muchos al platicar de software solamente hablan de Windows y office. Si alguien descalifica a Linux lo seguimos sin pensar, pero nos falta explorar. Debemos investigar he invitar a los chicos a que lo hagan y nos platiquen que han encontrado.
Así un día explorando en la red me encontré al Clubhouse, y ahora caminando juntos me encuentro con los clubs digitales.
Esto nos ayuda a que lo que soñamos lo hagamos posible. Si yo no se algo le digo a Marlene que me oriente y si quiero aprender las posibilidades de RPG le pido a Carlos que me eche una mano. Si actuamos solidariamente, creando el conocimiento, como un bien de todos llegaremos lejos.
Ahora si además de este apoyo que nos demos les proponemos juegos a los niños y los retamos a que lo hagan posible veremos que sus creaciones están llenas de sus sonrisas, de su esfuerzo de sus ganas.
Yo propondría que les inventemos un juego. Podría ser acerca del malvado virus AH1N1 (dirán que estoy enajenado, pero supongo que ninguno de ustedes cree que la sepa vino de Marte). En mi escuela estamos desarrollando un proyecto en el que tratamos de usar Scratch y los robots de Lego. Para este reto hemos leído el libro Triptofanito de Julio Frenk (quien fuera Secretario de Salud del sexenio pasado, vamos, no me vean azul, el era bueno, es un gran divulgador de la ciencia y como médico ha ocupado grandes puestos, actualmente trabaja en Harvard).
Podrían hacer animaciones en Scratch sobre la replicación de los virus. Armar un robot que busque cubrebocas y los lleve a una zona de un tablero donde podría estar pintada una nariz y una boca. O bien con RPG hacer todo un juego de este tipo.
De este tipo yo conozco Zelda, nunca lo he jugado pero he visto a mi hijo hacerlo. Zelda u otro personaje podría estar preocupado porque su aldea se encuentra atacada por la enfermedad. Entonces el buscaría a quien le indicara como poder ayudar a su aldea. Un personaje podría decirle que necesita Tamiflu para vencerlo pero para conseguirlo debe luchar. Antes necesita armas, es decir gel desinfectante, cubrebocas, alcohol y jabón. Estas las conseguiría comprándolas, pero el dinero lo obtendrá limpiando algún chiquero, repartiendo volantes sobre la enfermedad. Al tener estas armas podría dirigirse con algún malvado que no quiere darnos el Tamiflu pues quiere que escasee para venderlo al precio que se le pegue la gana y así dominar el mundo. Una vez vencido este malvado nuevamente nuestro personaje deberá conseguir dinero vacunando un determinado número de niños chillones, que no se dejen atrapar fácilmente, luego ir a una aldea a equipar un laboratorio cargando grandes aparatos y finalmente volver a luchar contra un malvado que represente a los intereses de las grandes compañías farmacéuticas que quieren hacer ellos las vacunas para venderlas al precio que ellos quieran. Al vencerlo nuestro personaje obtendría la vacuna que ayudaría a salvar las vidas de todos los habitantes del planeta.
Algo así podría ser el reto, usando quizás otros recursos tecnológicos que ustedes tengan a su alcance. Compartiendo sus resultados Si la idea prospera y conseguimos que los niños jueguen a esto, seguramente que lo que ellos produzcan será un gran tesoro que ellos habrán descubierto y en el que nosotros les habremos pasado las palas y los picos. Ellos serán los futuros científicos o los futuros artistas que hoy nos pinten un virus en Scratch. Y que mucha falta nos están haciendo como ya se vio en esta crisis
miércoles, 13 de mayo de 2009
¿Qué es una micra?
¿Qué es un amstrong?
Unidad de medida equivalente a la diez mil millonésima parte del metro, 0.000,000,000,1 metros, cuyo símbolo es Å, utilizada principalmente para indicar las longitudes de onda de la luz visible.
lunes, 11 de mayo de 2009
LOS VIRUS , BACTERIAS Y CRESIMIENTO EXPONENCIAL
Agentes infeccioso compuesto de ácido núcleo rodeado por proteínas y que solo se reproducen dentro de sus célula hospedadoras usando los órganos de estas.
BACTERIA
Las bacterias son microorganismos unicelulares que presentan un tamaño de algunos micrómetros de largo (entre 0,0 y 5 m , por lo general ) y diversas formas incluyendo esferas , barras y hélices
CRECIMIENTO EXPONENCIAL
El termino crecimiento exponencial se aplica generalmente a una magnitud tal que su variación en el tiempo es proporcional a su valor lo cual implica que crece muy rápidamente en el tiempo de acuerdo a la ecuación
martes, 5 de mayo de 2009
Saludos
Hola muchachos y antes que nada esperando que tanto sus familiares como ustedes se encuentren bien.
La contingencia sigue y los volveré a ver hasta el día 11 de mayo, así que trata de aprovechar este espacio para subir tus tareas, dudas o trabajos.
Algunos compañeros han publicado ya algún trabajo desde los primeros días y me parece que bajo las circunstancias actuales cualquier esfuerzo es muy apreciado por mí y seguramente también por sus papás.
Si puedes subir la información desde tu casa hazlo, pero no acudas a un café Internet sobretodo si es un lugar sin las normas de higiene que se están estableciendo.

La imagen es de: http://www.estrelladigital.es/ED/diario/129102.asp
Seguiremos en contacto por este medio, elabora una lista de dudas sobre esta situación en las que las matemáticas o la física puedan ayudar a dar respuesta.
Por ejemplo, estas pueden ser algunas dudas:
Por que usar jabón, cómo funciona el jabón para anular a los microorganismos.
Qué tamaño debe tener el virus de la influenza AH1N1.
Cuál es el radio del tejido de un cubrebocas.
Cuáles son los cubrebocas que deben usar los médicos que se exponen al virus, cuál debe ser el tamaño de la malla.
A qué distancia puede llegar un virus después de un estornudo. Trata de localizar algún video en cámara lenta sobre este fenómeno. Qué fuerza hace que no llegue más lejos.
Cómo podríamos matar a un virus si no están vivos.
Existen programas para simular una contingencia como esta y han ayudado a las autoridades para planear las medidas que se han tomado. También existen videojuegos en los que se simula un ataque de virus. Si tienes uno de estos juegos platícanos tu experiencia y si tiene datos trata de hacer una gráfica de muertos por unidad de tiempo.
Que es una gráfica exponencial. Busca las gráficas presentadas por las autoridades y observa como en un inicio esta influenza se comportó con un crecimiento exponencial.
Los chinos mandaron ayuda a nuestro país y el presidente fue al aeropuerto a dar las gracias. Pero a unos mexicanos al llegar a China los separaron. Esta actitud debida a su ignorancia ha generado indignación, no obstante por qué los chinos más que ningún otro pueblo, son más vulnerables a una pandemia.
Qué nos dice el mapa de la Influenza, el virus se desplaza. Hacia dónde lo hace. A qué velocidad.
Pronto nos volveremos a ver y con las investigaciones que hagas de estas y otras interrogantes, trataremos de analizar las respuestas. Cuida que los sitios de Internet que consultes sean serios, no digas que te lo mandaron en una cadena de mails. Trata que tu respuesta sea de algún científico reconocido, para ello busca el nombre de quien da la respuesta y donde trabaja.
Ahora debemos aprender a cuidarnos. Este es el primer ataque del virus y si nos sentimos triunfadores y bajamos las medidas de seguridad podemos hacer que el próximo ataque del virus sea más feroz.

Salud y un abrazo (acá de lejos).
sábado, 2 de mayo de 2009
EL CIRCULO
ÉS EL CONTORNO DEL CIRCULO
¿QUE ES EL RADIO?
ES UNA LINEA RECTA QUE SALE DEL CENTRO DEL CIRCULO ASIA CUALQUIER PUNTO DE LA CIRCUNFERENCIA.
¿ QUE ES UNA CUERDA?
ES UN SEGMENTO DE RECTA QUE TOCA DOS PUNTOS DE LA CIRCUNFERENCIA.
¿QUE ES UN ANGULO CENTRAL?
ES UN ANGULO QUE MIDE MENOS DE 90º Y QUE VERTICE TOCA EL CENTRO DEL CIRULO.
lunes, 27 de abril de 2009
¿Que es la circunferencia?
viernes, 24 de abril de 2009
EL CÍRCULO
En castellano, la palabra círculo tiene varias acepciones, la primera[1] : una superficie geométrica plana contenida dentro de una circunferencia con área definida; mientras que se denomina circunferencia[2] a la curva geométrica plana, cerrada, cuyos puntos son equidistantes del centro, y sólo posee longitud. "Aunque ambos conceptos están relacionados, no debe confundirse la circunferencia (línea curva) con el círculo (superficie)."[3]
Rectas y segmentos
Radio: es el segmento que une el centro y un punto de la circunferencia perimetral.
Diámetro: es el mayor segmento inscrito; pasa por el centro y divide al círculo dos semicírculos; es la mayor de las cuerdas de la circunferencia perimetral
.
Cuerda: es el segmento que une los extremos de un arco.
Recta secante: es la recta que corta al círculo en dos partes de diferente área.
Recta tangente: es la recta que toca al círculo en un solo punto; es perpendicular al radio cuyo extremo es el punto de tangencia.
Recta exterior: es aquella recta que no toca ningún punto del círculo.
miércoles, 22 de abril de 2009
EL CIRCULO

En castellano, la palabra círculo tiene varias acepciones, la primera : una superficie geométrica plana contenida dentro de una circunferencia con área definida; mientras que se denomina circunferencia , a la curva geométrica plana, cerrada, cuyos puntos son equidistantes del centro, y sólo posee longitud. "Aunque ambos conceptos están relacionados, no debe confundirse la circunferencia (línea curva) con el círculo (superficie)."
Puntos
Centro del círculo, que se corresponde con el centro de la circunferencia, del cual equidistan todos los puntos de esta.
Rectas y segmentos
Radio: es el segmento que une el centro y un punto de la circunferencia perímetro.
Diámetro: es el mayor segmento inscrito; pasa por el centro y divide al círculo dos semicírculos; es la mayor de las cuerdas de la circunferencia perímetro.
Cuerda: es el segmento que une los extremos de un arco.
Recta secante: es la recta que corta al círculo en dos partes de diferente área.
Recta tangente: es la recta que toca al círculo en un solo punto; es perpendicular al radio cuyo extremo es el punto de tangencia.
Recta exterior: es aquella recta que no toca ningún punto del círculo.
Curvas
Un círculo contiene infinitas circunferencias, siendo la más característica aquella que lo delimita, la circunferencia de radio máximo.
Superficies
El círculo también puede compartir con la circunferencia exterior los siguientes elementos: los arcos y sus cuerdas.
Sector circular: es la superficie delimitada por un arco y los dos radios que contienen sus extremos.
Segmento circular: es la superficie limitada por un arco y su cuerda.
Semicírculo: es la superficie limitada por un diámetro y media circunferencia.
Corona circular: es el espacio comprendido entre dos circunferencias concéntricas
martes, 21 de abril de 2009
°°°°EL CÍRCULO°°°°
PARTES DE UN CÍRCULO:
Centro del círculo, que se corresponde con el centro de la circunferencia, del cual equidistan todos los puntos de esta.
Radio: es el segmento que une el centro y un punto de la circunferencia perimetral.
Diámetro: es el mayor segmento inscrito; pasa por el centro y divide al círculo dos semicírculos; es la mayor de las cuerdas de la circunferencia perimetral.
Cuerda: es el segmento que une los extremos de un arco.
Recta secante: es la recta que corta al círculo en dos partes de diferente área.
Recta tangente: es la recta que toca al círculo en un solo punto; es perpendicular al radio cuyo extremo es el punto de tangencia.
Recta exterior: es aquella recta que no toca ningún punto del círculo.
Sector circular: es la superficie delimitada por un arco y los dos radios que contienen sus extremos.
Segmento circular: es la superficie limitada por un arco y su cuerda.
Semicírculo: es la superficie limitada por un diámetro y media circunferencia.
Corona circular: es el espacio comprendido entre dos circunferencias concéntricas.
 °°°°RETO°°°°
°°°°RETO°°°°Durante la clase de hoy pensamos en el reto del 5° periodo y es el siguiente:
°Hacer con los 43 alumnos que conforman al 1° d un circulo y marcar las principales partes de un circulo con la ayuda de objetos (por ejemplo globos).
°Todos esperamos que esto funcione por el momento pensaremos el el reto